Mathematical Induction Difficult Problems With Solutions
1 22 13 23 32 1 8 9 9 and I understand I have to get the sides to equal each other though Im not sure how to do that. DEPARTMENT OF MATHEMATICS UWA ACADEMY FOR YOUNG MATHEMATICIANS Induction.

Ib Maths Hl Questionbank Mathematical Induction
Prove by Mathematical Induction that nn 1n 2n 3n r 1 is divisible by r.

Mathematical induction difficult problems with solutions. R 1 n 2 r 1 n 2 f o r a l l n Z. So without further ado lets start. Put n 1.
Problems and Solutions in Mathematical. Induction problems can be hard to find. The first principle of Mathematical Induction points that when a base step and the inductive step are established as true it can be concluded that the initial statement Pn is true for all natural numbers.
By the Principle of Mathematical Induction Pn is true for all natural numbers n. Active 6 years ago. 12 23 34 n.
Hence 1 12 1 23 1 n1n 1 1 1 2 1 2 1 3 1 n1 1 n 1 1 n n1. Back them up with references or personal experience. N 1 n n 1 n 23.
2 Assume true for n k. Asking for help clarification or responding to other answers. 1 2.
Making statements based on opinion. Use mathematical induction to prove that for integer n n or to 2 x1n - nx - 1 is divisible by x2. Here are a collection of statements which can be proved by induction.
Fix k 1 and suppose that Pk holds that is 147 3k 2 k3k 1 2. 2903n 803n 464n 261n 1897 a n where an N. By the principle of mathematical induction prove that for n 1.
Using mathematical induction to solve a problem. Acces PDF Mathematical Induction Problems With Solutions Many students have trouble the first time they take a mathematics course in which proofs play a significant role. P1 1 3 2 3 3 3 1 3 11 12 2 1 1.
Prove the equality of. Start with base case n N and go backwards instead of starting at base case n 1 and going forwards. In this article we will discuss the remaining math solution problems and their solutions.
For any integer n 1 let Pn be the statement that 147 3n 2 n3n 1 2. Solving Problems in Mathematical Analysis Part I Mathematical induction along with its equivalents complete induction and well-ordering and its immediate consequence the pigeonhole principle constitute essential proof techniques. You can find ample problems based on this principle and their solutions in Mathematical Induction Class 11 NCERT Solutions.
Part I presents a general process for solving problems. 1 3 2 3 3 3 n 3 nn 12 2. For P1 2903 803 464 261 1897 1897 a1.
Let pn 1 3 2 3 3 3 n 3 nn 12 2. Hence p1 is true. The goal is to teach the reader how to proceed from an initial state of panic and fear to finding a beautiful and elegant solution to a problem.
Here are some possibilities. A few are quite difficult. 1 For n 1 we obtain a n a 1 r 1-1 a 1 so P1 is true 2 Assume that the formula a n a 1 r n-1 holds for all positive integers n 1 then.
Ask Question Asked 6 years ago. Sum _ r1 n 2r-1quad quad n 2 quad forquad allquad nin Z r1n. In the previous article we have discussed few Long Answer Type Questions 1i -xii.
The difficult ones are marked with an asterisk. N2 13 23. Its not a Homework problem.
3 Prove that the sum of the first n non-zero even numbers is n2 n. N3 Base case. Part II contains 35 difficult and challenging mathematics problems with complete solutions.
A Mathematical Induction Problem by Yue Kwok Choy Question Prove that for any natural number n 2903n 803n 464n 261n is divisible by 1897. The statement P1 says that 1 13 1 2. Induction Examples Question 1.
Problems with Solutions Greg Gamble 1. I would not ask you to do a problem this hard in a test or exam. Prove using mathematical induction that for all n 1 147 3n 2 n3n 1 2.
For all natural numbers n where r 1 2. I have a mathematical induction question and I know what I need to do just not how to do it. Thus x1k -kx -1 m x2 where m is any integer.
1 Prove for n 2 x12 - 2x - 1 x2 2x 1 - 2x -1 x2. Problems for Principle of Mathematical Induction. Mathematical Induction Problems With Solutions.
53 Someharder examples of mathematical induction Induction problems in stochastic processes are often trickier than usual. Most texts only have a small number not enough to give a student good practice at the method. Solution Let Pn be the proposition.
1 2 3 2 5 2 2n 1 2 n 2n 1 2n 13. This new edition of Vellemans successful text will prepare students to make the transition from solving problems to proving. Read PDF Mathematical Induction Problems With Solutions problems.
4 By the principle of mathematical induction prove that for n 1. Prove by mathematical induction that the formula a n a 1 r n-1 for the general term of a geometric sequence holds. Prove that for any natural number n 2 1 2 2 1 3 1 n 0 1 k 1 k1 k1k kk1 1 kk1.
Using the Principle of Mathematical Induction prove that. Every mathematician is familiar with mathematical induction and every student of. Difficult induction problem.

Mathematical Induction Practice Problems Youtube

Rd Sharma Solutions For Class 11 Maths Chapter 12 Mathematical Induction Download Free Pdf

Ib Maths Hl Questionbank Mathematical Induction

Ib Maths Hl Questionbank Mathematical Induction

Ib Maths Hl Questionbank Mathematical Induction
Proof Mathematical Induction Examples Payment Proof 2020

Ib Maths Hl Questionbank Mathematical Induction

Mathematical Induction Intermediate 1st Year Problems With Solutions Solutions For Mathematical Induction Inter First Year 1a Maths Glow

3 Mathematical Induction Pdf Free Download

Mathematical Induction Examples Solutions Youtube

Induction On Real Numbers Mathematics Stack Exchange
Https Www Stat Auckland Ac Nz Fewster 325 Notes Ch5annotated Pdf
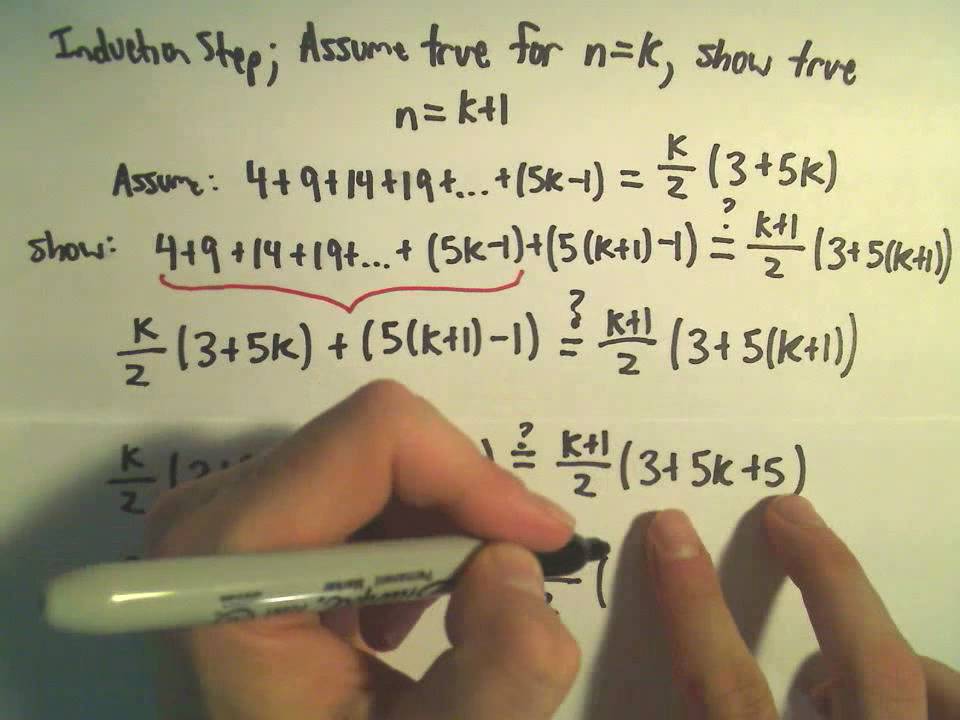
Recursion Sequences And Mathematical Induction Examples Solutions Videos Activities

Ib Maths Hl Questionbank Mathematical Induction
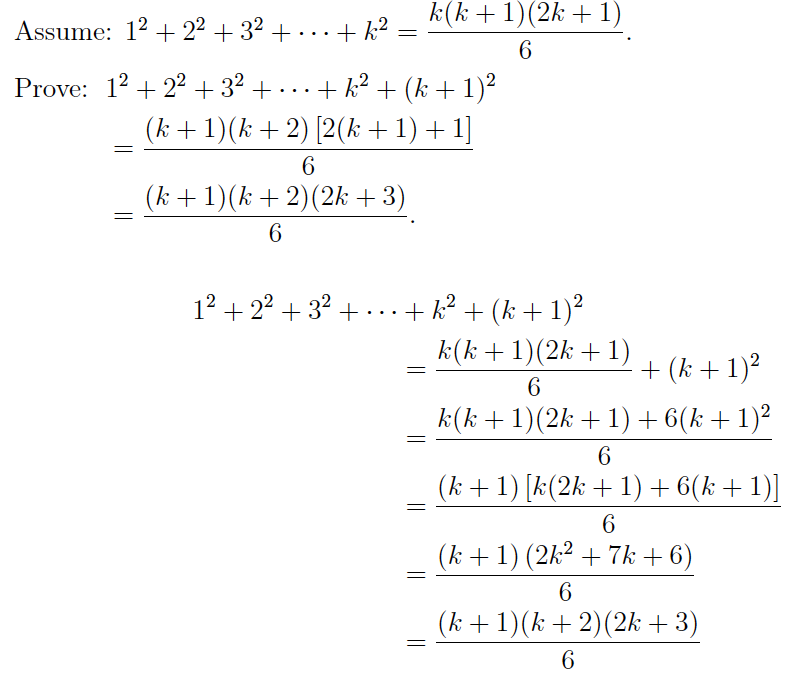
Principle Of Mathematical Induction Study Material For Iit Jee Askiitians

Proof By Induction Steps Payment Proof 2020
Https Www Gcsu Edu Sites Files Page Assets Node 808 Attachments Reid Pdf

Mathematical Induction Intermediate 1st Year Problems With Solutions Solutions For Mathematical Induction Inter First Year 1a Maths Glow
